Maps, the territory, and meta-rationality

The basic meaning of the metaphor is that representations (such as maps) do not perfectly reflect what they represent. Unthinkingly following an inaccurate map, you might try to drive to an island in the Pacific Ocean. Analogous mistakes are more common with other sorts of representations.

This essay uses the metaphor to introduce several key themes of In the Cells of the Eggplant. That is a book about how to improve science and engineering through meta-rationality: a better understanding of how rationality works in practice. The ways we use representations, and relate them with reality, are central topics. This essay may be a useful alternative introduction to the subject.

“The map is not the territory” is an important cautionary insight. However, it can also be a misleading metaphor. Maps are unlike most representations in significant ways, which we’ll explore in this essay. Specifically, many scientific and engineering models work in ways that are more complicated and different from maps. Unthinking application of the metaphor tends to reinforce simplistic “rationalist” theories of how technical work works.

In the course of the essay, we’ll develop more sophisticated understandings of rationality, truth, and science, and will introduce some themes of meta-rationality.

Bring meta-rationality into your orbit

This essay uses the Orbit spaced repetition system to help you learn and remember its contents. Orbit presents you with questions about the material as you read. If you create an Orbit account, or link to your existing one, it will send you occasional emails for review sessions that consolidate your memory.

I’ve written a metablog post about how I used Orbit to write this, and how you can use it when reading it. For this essay to be useful in your practice of rationality, and not just abstractly interesting, you’ll need to understand and remember its implications in situations where it is relevant. There’s solid evidence from cognitive psychology that spaced repetition dramatically potentiates learning. There’s also growing anecdotal evidence that it also produces deeper understanding.

If this gives you flashbacks to unpleasant memories of school quizzes, you can skip the Orbit blocks, of course!

(To see them, your browser needs javascript and cookies enabled. If you don’t see a big purple box right here, that’s why.)

A simple interpretation

Let’s go with the metaphor for a minute, and see what’s right about it, before exploring ways it breaks down.

Here are some commonly-cited cautions:

• Any map is likely to be wrong about some things. It might mark a one-way street in the wrong direction, or show a hiking trail crossing a gulch that is actually impassable.
• There will always be some uncertainty about whether a mark on a map is correct. Cartographers (map-makers) sometimes make mistakes. The data they start from are also always fallible and somewhat outdated.
• When you discover that the map you are using is wrong, you should update it.²
• No map can represent all the details of the territory—that is impossible, and also the map would have to be just as large, which would make it useless. You would do better to just look at reality. “The best material model of a cat is another, or preferably the same, cat.”―Norbert Wiener.³
• No map can be perfectly accurate, even at its scale. Wiggly lines never wiggle exactly the same way as the roads they represent. They are an approximation only.

Non-metaphorical versions of these limitations to technical knowledge are taught in undergraduate STEM classes, and probably won’t come as news for you.⁴

They make sense in a common rationalist explanation of how representations relate to reality. A theory, a model, or metaphorically a map, is a collection of statements that are either true or false of the territory. This correspondence theory of truth says that “snow is white” is true because “snow” means snow and “white” means white, and snow is white.

Applied to maps, it says that if there’s a horizontal line labeled “Fell Street” that goes from a line labeled “Market Street” to the green rectangle labeled “Golden Gate Park,” then the map is correct because Fell Street in San Francisco does run east-west from Market Street to the park. A map is a concise and convenient presentation of an equivalent collection of propositional statements.

Then “the map is not the territory” just means “the map does not necessarily provide the complete set of true facts about the territory.” Some of what it says may be false, or slightly off. In a probabilist framework, the caution is “don’t assign belief-strength 1.0 to everything the map says.” Also, it may offer no opinion about some things you care about: if they are too small, for example.

These considerations are valid and important to understand. High school may lead you to believe Science has all the answers; by the end of your undergraduate education, you should have realized that it doesn’t. Even having repeatedly discovered this, it’s easy to set aside your knowledge that the standard model of a domain leaves out important factors. (“It wasn’t my fault—everyone uses a Gaussian distribution!”)

In technical work, it’s common to develop a correct formal solution to a formal problem, and then be surprised when it doesn’t work in the real world. This is confusing the map with the territory. The aphorism is a useful warning against that.

Metaphors may mislead

“The map is not the territory” can be a valuable metaphor, but it can also be misleading. Most representations work differently from maps; and even literal maps work differently than in the rationalist interpretation of the saying.

Does this matter? Everyone does understand that “the map is not the territory” is only a metaphor. But metaphors shape thought. The phrase imports a mass of implicit, embodied experiences of using maps, and additional associated concepts and practices that “representation” and “model” don’t. That unhelpfully directs attention away from ways maps are atypical.

The relationship between literal maps and territories is also uncommonly straightforward. Taking maps as prototypes gives the mistaken impression that simply correcting factual errors, or improving quantitative accuracy, is the whole task of rationality. That omits most of what we do in science and engineering. If our metaphors pass over those parts, we will neglect them both in theory and in practice, and progress suffers.

Maps are used as a metaphor for a particularly simplistic version of the correspondence theory of truth. That theory is not outright false. It’s more-or-less true in many cases. However, it glosses over many complexities in representation/reality relationships. “Factually wrong” and “only approximately correct” are just two of the many possible shortcomings in a model. The metaphor becomes misleading if maps are used as the prototype for all representation.

Meta-rationality, investigating this question more seriously, finds diversity and complexity. We will explore several specific phenomena in representation/represented interactions here. Each shows a way the correspondence theory of truth is insufficient as an explanation of how representations work. Yet the list could be extended indefinitely; the details of representation/reality relationships are fractally unenumerable.

Because the map metaphor is misleading, it’s not ideal for explaining how either rationality or meta-rationality work. The Eggplant uses a variety of better explanations. I am expanding on this metaphor partly because a common reaction to hearing about the book is “isn’t this just saying that the map isn’t the territory?” So this essay explains how that is at most a starting point for understanding what it is about.

I’ll link to relevant chapters of The Eggplant you can read if you’d like to go deeper.

Nebulosity and more-or-less truth

As representations go, the relationship between literal maps and territories is exceptionally simple—at least in the idealized theory. The map is just a geometric scaling transform of reality. Objects on the map correspond one-to-one with objects in the world (down to a minimum size). There’s a constant proportionality of the distance between points in the territory with the distance between their representations on the map: just multiplied by the scale factor. And so on.

This idealized model is more-or-less true of a city street map. Cities pretty much are collections of clearly-delineated objects, such as roads, buildings, and parks, at the scale of a street map.

The model is much less true of a wilderness map. Those may use colors or symbols to indicate types of terrain, such as marsh, grassland, and forest. Marshes mostly do not have edges; they shade into grassland or scrub. There is no principled way of saying which category some points on earth belong in. A marsh does not have an exact shape or size.

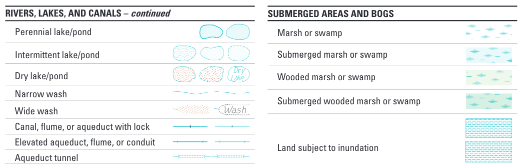
The illustration above is a bit of the U.S. Geological Survey’s Topographical Map Symbols brochure. You might find it fun to look through the whole thing (four pages). And you might consider the photograph of a marsh above… where would you draw the lines between the USGS categories “pond,” “submerged marsh,” “marsh,” “land subject to inundation,” “shrubland,” and “woodland”?

In many places there is no truth as to whether your choice is correct. This is not a matter of uncertainty. It is not that you do not know where the pond ends and the marsh begins, but that there is some Cosmic Truth about it. It is a matter of nebulosity: the territory itself is indefinite, neither one thing nor another. It’s only more-or-less true that the bottom half of the photograph above is mostly more-or-less marsh.

This is not to deny that maps, or other representations, can be wrong. Marking Death Valley as a marsh would be unambiguously false. Rather, I’m pointing out that “may be false” is not an full account of “the map is not the territory”—and beginning to explain some of the reasons.

Approximate truth

Wiggly lines on a map wiggle only approximately the same way as wiggly roads, I said. “Approximately” here may mean something very specific. If a map is accurate to within 10 meters, then there’s a numerical bound on how much the wiggles can deviate from reality. A statement is “approximately true” if it involves a numerical value that is wrong, but the true value is numerically close. Approximate truths are common in physics, and in the adjacent engineering fields. They are rare in most disciplines, including some science and engineering fields.

If you leave an eggplant long enough in a refrigerator, it eventually becomes a non-eggplant. (Eww!) At what point does “there is an eggplant in the refrigerator” cease to be true? At intermediate times, this is not “approximately true” in the sense of a numerical error bound.

Genes are interesting to geneticists, but what counts as one is notoriously impossible to define.⁵ Examples of “sort of” genes—marginal cases under a definition—are common. However, a particular bit of DNA is never “approximately” a gene, in the sense of “to within an error bound.”

The chapter “Overdriving Approximation” in The Eggplant has more on why approximation is an inadequate understanding of more-or-less right explanations.

Localities and non-locality

Because bits of a map correspond to locations on the earth’s surface, a bit of the map is accurate or inaccurate all on its own. The rest of the map (and the rest of the earth) is irrelevant. If Las Vegas sprouts a new suburb, it doesn’t invalidate a Nevada map’s treatment of Reno. This is not typical for representations in general, nor for technical models in particular.

Often unenumerably many factors are relevant. A good model can take only some of them into account, but even so it is accurate or inaccurate only overall, not piece-by-piece. The individual bits of the model may be meaningless without the rest.

In cell biology, pretty much everything causes pretty much everything else. You can’t understand parts of a cell accurately other than in terms of other parts. This is not an undifferentiated New Age wow-man holism; different parts affect each other in different ways and to different extents. But everything is somewhat relevant, and almost anything could be affected by a missing or mistaken understanding of almost anything else.

Locality makes it easy to check whether a particular bit of a literal map is accurate: you can just go there and see. Most scientific theories can’t be evaluated locally. Taking “map” as a metaphor makes you blind to the problem of “confirmation holism”: individual hypotheses can never be tested experimentally, because unenumerable additional factors might be relevant.⁶ You have to assume that your experimental apparatus works as you believe it to, that your materials are what you think they are, and that you have controlled for all unexpected sources of systematic variation. Achieving this as an absolute is impossible in theory, and achieving it adequately is difficult in practice.

A classic example of the problem was the mid-19^th century discovery that the orbit of Uranus does not accurately conform to Newtonian mechanics. Either Newton was wrong, or something else. Unenumerable “something else”s are imaginable. Astronomers guessed that there might exist a previously unimagined planet perturbing Uranus’s orbit—an unexpected, non-local source of systematic variation. Based on the specifics of the anomaly, they predicted its location, velocity, and mass, and pointed a telescope there, and thereby discovered Neptune.

Uranus’ anomalous orbit didn’t prove Newton wrong, but neither did the observation of Neptune prove him right. And of course, he was wrong. Mercury doesn’t conform to Newtonian mechanics either—in that case due to Einsteinian relativity.

“The Spanish Inquisition” and “The probability of green cheese” discuss this problem further. “Reductio ad reductionem” explains why reductionism does not solve it. “Are eggplants fruits?” explains why you cannot even define the meaning of biological terms other than as part of an unbounded web of other terms for other biological phenomena.

The map can’t do the work for you

We went cross-country skiing. They gave us a paper map. (I guess XC is a sport for old people?)

The map was… less helpful than ideal.

In Days Of Yore, streets in some regions had signs at every junction saying which they were. Then you could find them reliably on your map.⁷ The XC trail system did have some signs scattered about… mostly not where you’d want one… and sometimes halfway between two trails, at a junction, so it wasn’t clear which it referred to.

More than once, we spent several minutes looking back and forth between the map and the territory, trying to figure out what it was trying to say. Everything on both was either snow or a pine tree, so it wasn’t obvious. We’re at a trail junction… but which? Is that hill this thing on the map? Or is it that one? Does it even count as steep enough to belong on the map? Is the bend we just came around that squiggle, or is it too sharp, and it must be something else?

The point here is not that the map was bad (although it was). It’s that, no matter how good a map is, it still takes work to figure out what it means for what you’re doing.

This used to be a constant hassle with paper maps. GPS direction-giving systems automate much of that work, but their instructions are still sometimes annoyingly ambiguous, and you wind up taking the wrong turn.

“Instructed activity” in The Eggplant expands on this theme. A good example is assembling flat-pack furniture. Locating the bits referred to in the instructions is notoriously difficult. (Is this “Snap fastener (J)” or “Plastic insert (C)”?) Often the question is “what is this even trying to say?” The instructions are a representation—a “map”—of what you are supposed to do, but they won’t do it for you. You can’t just “follow the map,” because much of the time it makes no sense—until you get it figured out.

Glossing over the details of how we relate representations with reality is a major failing of rationalism. Part One of The Eggplant discusses this absence of explanation extensively, starting in “Reference: rationalism’s reality problem.” Much of Part Two explains work we do to connect representations and reality; “Meaningful perception” could be a good starting point. The correspondence theory of truth is a nice idea, but there are no correspondence fairies magically bridging the metaphysical gap between maps and territories for us.

As with maps, to use a rational model, we have to relate it to reality. Mostly this is concrete practical activity, not formal problem solving. The Eggplant calls this hard work circumrationality, and it is a major topic of Part Three. That Part isn’t written yet, but there’s a summary discussion of circumrationality here.

Circumrationality may involve informal reasoning, but it’s usually more a matter of perception and action. Taking the ski map as a metaphor for a rational system: our using it required the circumrational work of looking back and forth between it and the pine trees, discussing our guesses about where we were, and going a few hundred yards along a plausible trail to see if an expected landmark showed up.

Popping out of the metaphor, circumrationality is the work of identifying the physical phenomena a rational system’s formal objects refer to, and carrying out the actions it calls for (but underspecifies).

Circumrationality is generally routine. It does not require significant understanding of the rational system itself, only of how a particular, perhaps tiny part of it relates to the job at hand. Circumrationality is not necessarily easy, though. It may involve extensive inexplicit, bodily skills. Often that makes it harder to automate than rationality, whose skills are mainly explicit, and therefore easier to encode in a computer program.

Systematicity and completeness

As a cartographer, you can systematically survey a city and be effectively certain your map isn’t missing anything. You aren’t going to learn next year that there’s a Narroway in Manhattan, running parallel to Broadway, that you somehow overlooked. You aren’t going to discover an entire secret system of Manhattan streets running 45 degrees to the grid you knew about.⁸

Such systematicity is atypical. In most domains, you can expect there are significant features, and types of features, you don’t know about at all. An example is the 2015 discovery of the meningeal lymphatic vessels, a system of tubes that drain waste from the brain. This anatomical feature had been overlooked, and it was explicitly believed that nothing like it existed. Until 2015, it was thought that the brain had no lymphatic system, and waste could only be eliminated by passive diffusion. It’s now known that the brain is “washed” during sleep by actively pumping fluid through it and flushing into the meningeal lymphatic vessels. It’s now considered that malfunctioning of this system may be the cause of multiple degenerative brain diseases, such as Alzheimer’s.

Is there a there there?

With a literal map, you know there is a territory, and which one it is. It could be a lousy map, but it’s definitely a map of something, and you know what.⁹

In science, it’s frequently unclear what a model is a model of, or even whether it’s a model of anything. Figuring that out often constitutes major scientific progress.

A famous case is polywater, an unusual form of water with fascinating properties, consistent with the theory that water molecules get polymerized into chains. Lots of experiments measured these properties precisely and explored practical applications. Eventually it turned out that there was no such thing; supposed “polywater” was ordinary water contaminated during sample preparation.

When I studied molecular genetics, the professor told us confidentially that “Okazaki fragments”—short bits of DNA extracted from bacteria—were not a thing. They were a hot topic at the time, but he said they were just artifacts of sloppy sample preparation that broke up chromosomes, not biological phenomena in living cells. Reading the Wikipedia article now, it seems he was wrong. They are totally a thing.

A current open example is “ego depletion.” It seems that willpower is a limited resource, and it gets used up in difficult, unpleasant tasks. Hundreds of experiments have found factors that increase or decrease the rate of depletion, explored its physiological basis, and measured it using objective EEG methods.

Recently, larger, more careful experiments suggest that there is no such thing.¹⁰ Apparently, the detailed, scientific map of the ego depletion territory is a map of Narnia.

But, everyone’s personal experience suggests that there must be such a thing; we all experience it at the end of a long tiresome day.

This is currently up for grabs. Ego depletion now seems to be mostly not a thing, but maybe somewhat a thing, but it’s not clear what sort of a thing it is, probably a different sort of thing than people thought five years ago, or maybe it’s several vaguely similar things, and anyway the hundreds of papers were all pretty much nonsense (probably?) because the thing that people thought it was mostly isn’t one.¹¹

Different maps for different trips

A road map is useless when you are going for a hike. You need a topographic map that shows trails, altitudes, streams, and peaks. Road maps and topographic maps are both useless in a seismic safety analysis. For that you need a map that shows geological formations, soil types, and faults.

These three kinds of maps express three different ontologies of the same territory. By “an ontology” I mean a system of categories, properties, and relationships you ascribe to the world.¹² In the map analogy, it’s the set of symbols and features the cartographers chose to limit themselves to.

Which ontology is useful depends on your purpose. Ontologies are not theories; none of them is more or less “true” or accurate than the others. They are largely incommensurable. They describe the same territory, but they do not contradict; the ways they portray the world are just different. This is characteristic of ontologies. Consequently, accurate representations are only accurate in a particular sense, and for particular purposes; and different representations of the same phenomena may be accurate in different senses.

… Oof! That got pretty thick. I’m thinking it must be time for an entertainment break. This video makes many of the same points as my essay—including this point about different sorts of maps—and it’s way more fun!

… OK, back to business.

With literal maps, it’s generally obvious which sort to use for a particular purpose. This is often not true when using rational models. A major aspect of meta-rationality is figuring out an appropriate ontology for a particular job, and what sort of model to use within that ontology.

A typical rationalist failure mode is overlooking the necessity of making this choice explicitly. It’s common instead to apply an ontology by default, without thinking about it. Tacitly assuming a Gaussian distribution is a common, sometimes famously disastrous example.

Can’t you combine all map types, to make a more complete, more accurate model? In fact, shouldn’t a map ideally show features of all sorts, to be useful for all purposes? No; that would make an unreadable mess. There can be no overarching universal ontology, combining all possible categorizations. That is an infinite task—impossible in principle, infeasible in practice, and useless if somehow achieved. It’s like the fantasy of a perfectly detailed, but unusably enormous, map.

Sometimes you can combine a few, carefully-selected ontologies into a broader framework.¹³ Sometimes that is useful. Sometimes it’s infeasible; often it’s just confusing. Figuring that out is a meta-rational operation.

Beyond choosing or combining existing map types, a novel task type sometimes demands an entirely new one. When the augmented reality game Pokemon Go came out, suddenly everyone wanted to know where to find PokéStops—places in the real world where you could find monsters and treasure in the virtual one. Entrepreneurs created web sites that superimposed that information on Google Maps. Analogously, meta-rationality may involve developing a new ontology.

These are all issues that “the map is not the territory” tends to draw attention away from, by suggesting that the only issue is whether the map is accurate.

The Eggplant describes this mistake as “being an oblivious geek.” That is failure to notice that a rational system is not interfacing well with its context.

It is like “confusing the map with the territory,” but at a more abstract level. Rather than assuming that you map you have is accurate, you assume that the type of map you have could be made adequate through rational/empirical improvement. But you can’t make a road map usable for mountain hiking—not without expanding its ontology to include an entirely different set of features. You can’t accurately predict planetary movements with any finite combination of circular motions, nor financial market movements with any finite combination of Gaussian distributions.

An as-yet unfinished section of The Eggplant will explain how to notice this obliviousness when you make tacit ontological choices, and how to correct it. In short: the antidote to oblivious geekery is to apply meta-rationality.

Fitting the territory to the map

Maps, and other simple models, work best when representing standardized, engineered artifacts, such as roads. Those are designed to minimize nebulosity. By and large, either there’s a road there, or there isn’t. Mostly we don’t build vague sort-of roads, because they wouldn’t work reliably.¹⁴ Mostly, we give specific names to roads, and put those on the map; there is usually no ambiguity about which road you are on.¹⁵

Much in reality—like marshes—isn’t like this. The territory doesn’t come neatly divided into objects with standard names and unambiguous properties and relationships. Often, simple models can only be simplistic, i.e. wrong. With increasing complexity and nebulosity of phenomena, effective understandings become increasingly dissimilar to literal maps.

Sometimes, when the map doesn’t fit the territory, it is easier to fix the territory than the map! We reshape our environment to fit our categories.

This is literally true when a municipality or development company plans a new residential subdivision. They draw a road map, and send in bulldozers to make the territory conform to it.

More generally, engineering design often produces a map-like representation—a blueprint or circuit diagram—that a manufacturer makes bits of reality conform to. Still more abstractly, manufacturing standards and specifications, even if not geometrical or topological, are models that we make reality match.

Meta-rationality at a ski resort

Deficiencies in a rational system often show up first in circumrationality. You can’t identify the real-world objects or properties the formalism supposedly refers to; or the actions it calls for make no sense in context due to factors it does not take into account. When you notice circumrationality breaking down, because it’s too difficult to bridge the representation/reality gap—it’s time to get meta-rational!

The work of many technical professionals is done entirely within abstracted formal representations. In that case, you may have little motivation to understand how those representations relate to reality. Being an oblivious geek works just fine, so long as someone else does the work of translating real-world problems into your formal language and your formal solutions into real-world work. That translation requires a quite different skill set: meta-rationality.

Circumrationality and meta-rationality both operate at the interface between a rational system and its surrounds, but differ in scope.

• Circumrationality takes the rational system as given and immutable, and relates it to concrete circumstances in order to get a particular job done.
• Meta-rationality stands outside a rational system, surveys its operation as a whole from above, understands its relationships with its broad context, and intervenes to modify the system and/or its surrounds so they work better together.

Literal maps can be a misleading metaphor for rational models, and they are even less good for explaining meta-rationality. But at this stage in the essay, we are committed! We have skied deep into a wilderness of tangled metaphors where everything looks like a map. So let’s try to follow the metaphor, and see if we can find our way home…

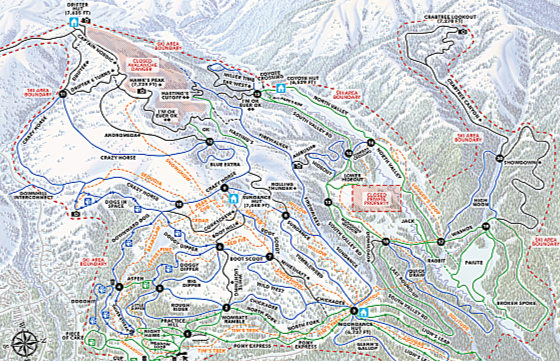
I would guess this map was produced by technical professionals. Probably mainly a graphical designer, perhaps in collaboration with an actual specialist cartographer, plus at least one marketing professional, likely at the executive level.

Presumably everything on the map is true. Every trail it shows actually exists, and is where it says it is, and every trail maintained by the ski resort does appear on the map. This, by analogy, is the work of rationality.

And it achieved rationalist nirvana: a complete and entirely correct map of the territory!

But to the extent that the professionals involved overlooked the difficulty of finding yourself on it, they were being oblivious geeks.

A common form of obliviousness: the rational professional who solves a formal problem has no experience with the circumrational use of the system, and so does not realize that their “solution” doesn’t work in the real world. In this case, it seems likely that the ski resort hired an outside graphic design firm to make the map, and the designer had never been there, or at any rate never tried to use their own map.

A ski map is not really a “rational system,” but we can imagine the ski resort’s map team addressing the difficulty we encountered in ways analogous to rationality and to meta-rationality.

Rationality works within a system to solve problems. By analogy, the map team might try adding more details. If specific stands of pines were shown clearly enough to be recognizable, it might solve the problem! But it might become unusably enormous. Analogously, a common rationalist approach to trouble in applying rationality is to elaborate the system. That can work, or it can produce unmanageable internal complexity.

Here are some approaches the team might take after stepping out of the “we have to make a better map” assumption, and considering the problem in its broad context. I’ve labeled each response with the meta-rational operation it corresponds to; these and many others will be explained in detail in Part Four of The Eggplant.

• Is this problem important enough to bother with, or is it better left unfixed? Does it annoy enough visitors enough that they don’t come back, or bad-mouth the resort to their friends? Can we put a rough dollar value on that? How much do we care about their enjoyment, quite apart from our financial incentives? [Reflection on purposes]
• Do we have the right kind of map? Would it be better to offer visitors a GPS map, automatically eliminating the “where the heck are we” problem? Would they prefer that, or do they really want paper? [Evaluating alternative systems and selecting one]
• Maybe some want paper, and some GPS, so offer both? [Combining two rational systems, as a patchwork, not as a synthesis]
• Maybe it would be better to fix the territory than the map? If every trail junction was clearly signed, would that solve the problem? [Meta-rational interventions can be in a rational system, or in its surrounds, or both]
• Is a map even the right approach? Who wants to have to stop skiing and take off their mittens to fumble with a map or smartphone every three minutes, anyway! Maybe more fun and less confusing would be a GPS-aware ski-buddy phone app that, based on your skill and energy level and adventurousness and the time of day and current trail conditions, would choose a route for you, and give you verbal directions at junctions? [Inventing a new rational system]
• “The best model of a cat is the same cat.” If we built numerous skiable overlook platforms that let you see the trail system from above, maybe that would be more fun and useful than any representation? [A radical switch of ontology]

Well-motivated misleading

“The map is not the territory” can be a misleading metaphor. That’s not an accident; the misleading is motivated by a desire for an emotionally comforting simplicity and certainty. However, depending on where you are at in your relationship with rationality, the misunderstandings it produces may be helpful, and the motivation may be good.

In learning to use rationality effectively, we pass through four qualitatively different understandings of what it is and how and why it works. Each is more sophisticated and less wrong than the previous one, but also more difficult both cognitively and emotionally. Teaching rationality well requires explaining it at the level a pupil can understand—even when those explanations are, in some ways, radically false.

High school classes give the impression that Science!™️ is a collection of proven Truths that explain everything about how the world works. This is easy to understand, and emotionally reassuring. High school students are mostly not ready for a more accurate presentation. However, high school STEM classes do teach you formalism: how to manipulate meaningless symbols according to non-negotiable rules.

During undergraduate and maybe Masters’ level STEM education, you gradually understand that scientific and engineering knowledge is uncertain and incomplete. “The map is not the territory” is a helpful reminder here. Yet at this second stage—which we could call basic or routine rationality—you still believe that The Scientific Method™️ is a straightforward and reliable way to incrementally reduce uncertainty and fill the gaps in the map.

Maybe you have noticed that “the map is not the territory” applies to itself? The map/territory relationship is itself a “map” of the “territory” of representation/reality relationships in general. In some parts of the “territory” it’s accurate enough to be useful; in others, it’s worse than useless.

It is common to confuse this “meta-map” with the territory of scientific and engineering work. That is, to suppose that doing science consists merely of cartography, of finding definite truths within a set scheme of map symbols; and that doing engineering consists merely of deriving designs from known truths. Both those activities are important, but they are a small part of what scientists and engineers do—both in terms of effort and of value produced. (In practice, most of our effort goes into improvising methods for making recalcitrant equipment do what we need. The greatest value we produce is novel ontology—better ways of understanding what there is and can be in the world—not truths.)

Thinking in terms of “maps” rather than “representations” greatly simplifies the conceptual problems of epistemology—belief, truth, and knowledge. It’s an appropriate metaphor at the level of basic rationality. It provides a clearer, cleaner (but less accurate) understanding of the model/reality relationship than those appropriate to later stages. It gives the impression that science and engineering are much more tractable than they actually are. That, again, is emotionally comforting relative to the more sophisticated views. “Rationalism,” as The Eggplant uses the term, is the emotionally-motivated insistence that this view is True. Adopting it can get you stuck at the stage of basic rationality.

Rationalism and The Scientific Method are fairy tales you have to let go of to move on to the next stage, advanced or adventure rationality. There you realize there is no method, only methods. You realize that science and engineering knowledge can mostly only be more-or-less truths, because reality itself is inherently nebulous, so there are few if any Truths to be found there.

If “the map is not the territory” is understood as “maybe not everything it says is true,” then the metaphor may be a misleading hindrance to making this transition. If it is understood as “the territory is nebulous, whereas the map is not,” it could propel you forward.

Adventure rationality is analogous to going places where no map is available, or only a sketch map. It means exploring marshy bits of reality where there are no solid facts to stand on, where no crisp ontology is possible, where the shore gets lost in fog, where not only is there no map but it isn’t even clear if there is a territory—and you emerge with a rational solution anyway. You have left “the map is not the territory” far behind. That’s kid stuff now.

Meta-rationality accepts the even more emotionally difficult absolute groundlessness of unrestricted reality. The entire universe is a marsh; there is no dry land to emerge to. Abiding in the marsh, you may create rational solutions, or non-rational reasonable solutions, or mythic solutions. Or you may observe that “problems” and “solutions” are both ludicrous fictions; marshes don’t work like that.

You may create a tasty breakfast or a billion-dollar tech company or a new religious movement. You may draw a map or a mermaid. You may use the map as fish wrap or as a cryptographic one-time pad or fold it into a hat or proclaim that it is the rightful Emperor. Sober technical people may eventually realize that your proclamation was rational and correct and important.

And so on, and so on

This essay is too long. And at the end of the last section, it got too silly. It could get much longer, and perhaps even sillier.

It could be a book—but there is a better one.

I have been working on this piece, on and off, since 2014 I think. Once or twice a year, I’ve been reminded of it, and thought “I really ought to finish that,” and put another couple days work into it, and concluded once again that it is unfinishable.

Why?

I had two goals. First was to show how using maps as a metaphor for all representations was a motivated choice, because it falsely reassures rationalists that the difficulties in their theories of representation are tractable. The second was to illustrate a more accurate understanding of representation with more realistic examples of real-world map use.

This plan had two fatal flaws.

First, these goals conflict. “The map is not the territory” can be reassuring only because maps are highly atypical as representations. That makes them bad examples for use in a better explanation.

The second problem is that the actual relationships between representations and reality are unenumerably diverse. Once you start explaining them, there’s no logical stopping point. You can keep on pointing out relevant phenomena indefinitely. “How we refer” makes this point by listing “a bunch of stupid referring tricks, quickly; our job here is just to get a sense of their diversity, not to do proper ethnomethodology, much less science.” Having finally realized this, I can just stop, rather than continuing to attempt an impossible comprehensive systematicity.

Both problems are better addressed in The Eggplant—which I began writing in 2017, well after the first few times I’d given up on this essay. Its Part One gives a detailed explanation of why the rationalist theory of representation is wrong, using better examples. Parts Two and Three provide a better explanation of how representation does work, using better examples. Parts Four and Five show ways we can do rationality better with a better understanding of how it relates with reality.

Thanks

Special thanks to Lucy Keer who read approximately 6.02×10²³ drafts of this thing, and said useful and encouraging things about them.

And to Lucy Suchman, who taught me what little I know about ethnomethodology. Her discussions of maps in Human-Machine Reconfigurations provide the root text for this essay.¹⁶ I wouldn’t have understood the point if she hadn’t patiently explained it to me in person.

And to Andy Matuschak for creating Orbit, and for tutoring me in its use.

And to Basil Marte for recommending the Map Men video which provided our entertainment break. You have watched it, haven’t you?