Part Three: Taking rationality seriously

A temporary overview

As of mid-2020, Part Three, which explains how rationality works, is unfinished. This temporary web page is an extensive summary of its contents.

This summary is about 6000 words, equivalent to 15–20 printed pages. I expect the full, finished Part will be a bit over a hundred pages—to give you a sense of how much more detail it will provide. I hope this summary is detailed enough to give a useful overall understanding.

This summary also frequently foreshadows the contents of the unpublished Part Four. That explains how meta-rationality can improve our use of rationality by reflecting on the explanations in Part Three.

Taking rationality seriously

“Taking rationality seriously” means caring enough about it to want to improve its operation. That requires an empirically accurate and practical understanding of how and when and why rationality works.

We saw in Part One that most theories of rationality (rationalisms) involve impossible metaphysical fantasies, and encounter frequent difficulties in practice. A better explanation should address all those problems, explaining how rationality (as a real-world practice) successfully handles each issue.

This Part of The Eggplant presents such an alternative understanding of rationality, using a meta-rationalist approach. That is: observing the operation of rationality from outside and above, rather than trying to make sense of it from inside.

Part Three is the middle of the book. As such, it ties both back and forward, to all the other Parts.

Looking back, it explains how its alternative understanding of rationality deals with each of the difficulties rationalism faced, as explained in Part One. It also shows how each of the resources provided by reasonableness, explained in Part Two, contribute to rationality’s functioning.

Looking forward, Part Three provides a necessary “anatomy” or “engineering diagram” of rationality. It explains what rationality’s major moving parts are, and how they relate. Some pieces critical to its operation are entirely overlooked by rationalist theories. An accurate explanation is a prerequisite to understanding meta-rationality, because that acts on rationality to modify its operation. The “floor plan” of rationality shows sites where meta-rationality can intervene. For example, the interface between rationality and reasonableness is one of the most important sites for intervention, and rationalist theories don’t even recognize its existence.

Part Three foreshadows themes of Parts Four and Five. Those are the heart of The Eggplant, because meta-rationality is its overall topic.

• Part Three points out difficulties in the use of rationality that rationalism cannot address, but which are resolved meta-rationally in Part Four.
• Part Three also concerns rationality as a professional practice. That is the topic for Part Five. Part Five takes an explicitly meta-rational approach, whereas that is only hinted at here.

Although the primary function of Part Three is preliminary, it may also be interesting in is own right, for understanding your personal practice of rationality. As technical professionals, we are fascinated with the tools we rely on: GC/MS instruments, 3D printers, bytecode compilers. Rationality is our most important tool, and you may be excited to gain a new understanding of how it works.

What an understanding of rationality should do

An understanding of rationality should explain—to the extent possible—how, when, and why rationality works.

• It should account for observed facts about how rationality works in practice.
• More important: it should be useful. An abstract descriptive theory might be academically interesting, but rationality is too valuable to leave it at that. A better understanding than rationalism ought to enable us do rationality better.
• As a secondary, aesthetic consideration, it should also eschew metaphysics, and prefer naturalistic explanations, where possible.

The standard rationalist story of how rationality guides practical work goes like this:

• You make a formal model of the problem (abstraction)
• You use rational inference within the formal model to solve the problem (problem-solving)
• You apply the formal solution to the real-world problem (application).

This is not exactly wrong, but it leaves open key questions:

• Specifically how do you get a formal model, starting from a real-world situation?
• What sort of thing is a formal model?
• How does the abstract formal model relate to the concrete situation? In two senses: how can abstract and concrete things relate at all; and how does this particular abstraction relate to that particular situation?
• If the formal model is an abstraction, how do you relate to it, given that you are physical and it apparently isn’t?
• What does problem-solving consist of? How do you do it?
• Given a formal solution, how do you make use of it in the real world?

The overall issue here is: How do abstractions, which seem to be metaphysical, relate to physical reality? Rationalism has no answer (as we saw in Part One).

STEM education, at least before the PhD level, is almost entirely about problem solving within a rational system. You are given an abstract, formal model, supposedly of some real-world phenomenon, which you are supposed to take for granted. You are given a formal problem statement within the abstraction, and you manipulate it according to formal rules, in order to produce a formal solution, which is an abstraction that matches the specification. Then you are done.

Most contemporary rationalists are passionately committed to materialism, which makes questions about “how does all this abstract stuff relate to reality” especially awkward. So STEM education tacitly teaches you not to ask these questions, by declaring them philosophical nonsense with no meaningful implications for technical work. The implication is that, in practice, such issues are trivial for scientists and engineers, even if they might cause trouble for philosophers.

Part Three suggests that each of the “philosophical” questions, raised above, represents a concrete, practical task within rational practice. Reflecting on how you do them (which constitutes meta-rationality) can improve that practice. Passing over these considerations can produce predictable patterns of rationalist failure.

The J-curve of development

Understanding how individuals develop into rationality, and then into meta-rationality, helps understand what rationality and meta-rationality are. Although personal development is a continuous process, it can be helpful to think of it as divided into stages:

• Pre-rationality: you can be reasonable, but have little or no capacity for formal reasoning.
• Developing formality: you learn how to conform to formal, rather than reasonable, norms. Mastering the high school mathematics curriculum is adequate.
• Basic rationality: you learn how to model the material world using formal systems with routine, conventional patterns of correspondence. Undergraduate STEM education teaches this.
• Advanced rationality: you figure out how to deploy rationality in cases where standard conventional patterns don’t apply. This is the functional prerequisite for competence in senior science, technology, and engineering jobs. (And in other rationality-based occupations, such as business, public administration, and law.) Graduate school may transmit it, usually mainly informally. It shades into meta-rationality.
• Meta-rationality: Dynamic revision of rational, circumrational, and meta-rational processes through meta-rational understanding. This is not taught. Rarely, it is transmitted through apprenticeship, in the course of a PhD, or on the job. Mostly you have to figure it out for yourself, though reflection on experience of practice.

Part Three covers the three middle stages of the list, in order: formality, basic rationality, advanced rationality. This sequence is compatible with a developmental model I’ve presented elsewhere. Part Three elaborates and subdivides the path into, through, and beyond the “systematic” stage of that schema.

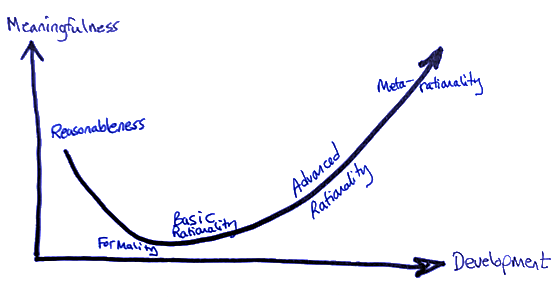
I describe development from reasonableness through rationality to meta-rationality as a “J-curve,” with time on the horizontal axis and the role of meaningfulness—context, purpose, and nebulous specifics—on the vertical.

We saw in Part Two that context, purpose, and nebulosity are essential to reasonableness. (That is the leftmost part of the J.)

Eliminating meaning is essential to formality. Rationality gains its power from transcending context, purpose, and specifics, to create universal, abstract, general systems. The first step in developing rationality is accepting this unnatural, emotionally difficult operation. You have to become comfortable with meaninglessness.

“But I don’t get it,” the student struggling with high school algebra protests. “What does ‘x’ mean?” It doesn’t mean anything. That is the whole point. That meaninglessness is why formalism works. You cannot get this by learning facts, nor procedures, though both are necessary.

To become rational, you need to become a fundamentally different sort of process yourself—a sort that seems rigid, cold, and alien until you have made the transition. A sort that can wield the power of meaninglessness.

The J bottoms out as you learn to strip context and purpose off the real world, treating it as collections of abstractions. You learn to deal with struts, enzymes, populations, and economies on the same basis as polynomials. This is basic rationality.

As you develop through advanced rationality and into meta-rationality, context and purpose come back into play. The right end of the J is taller than the left, because meta-rationality takes an enormously broader view than mere reasonableness. It considers contexts and purposes with potentially vast scope across space, time, and complexity—whereas reasonableness is sensitive only to the mundane aspects of the immediate situation necessary to get a particular job done now.

This second developmental transition is also emotionally difficult. The vastness and groundlessness of the meta-rational way of being provoke agoraphobia and vertigo. Again, to get meta-rationality, it is insufficient to learn new concepts and methods. You must become a qualitatively different sort of space yourself—one that seems unacceptably unbounded, indefinite, and alien until you have made the transition.

Formalism

Rationalism’s theory of problem solving is that you manipulate abstract objects according to formal rules. Undergraduate STEM education mostly teaches you those rules. But how can you, a physical object, manipulate metaphysical, abstract objects?

The implicit story is that you sit back, close your eyes, enter the rationality trance, and mentally step through the Pythagorean Portal into the Metaphysical Realm of Pure Forms. In your astral body, you quest amongst the quaternions; your etheric eyes survey the serried rows of the regression matrix; with your ghostly hands you invert cyclic subgroups like phantom bicycle wheels.

In the chapter on advanced rationality, we’ll see that this is not entirely wrong—although obviously uncomfortable from a physicalist standpoint. However, it’s empirically false as a theory of formal problem solving in basic rationality.

Fortunately, a naturalistic alternative is available, and it also helps explains how and when and why rationality works.

Humans evolved for reasonableness, not formal rationality. Unaided, we are almost entirely incapable of it. We need artificial cognitive support:

The physicist Richard Feynman once got into an argument with the historian Charles Weiner. Feynman understood the extended mind; he knew that writing his equations and ideas on paper was crucial to his thought. But when Weiner looked over a pile of Feynman’s notebooks, he called them a wonderful “record of his day-to-day work.” No, no, Feynman replied testily. They weren’t a record of his thinking process. They were his thinking process:

“I actually did the work on the paper,” he said.

“Well,” Weiner said, “the work was done in your head, but the record of it is still here.”

“No, it’s not a record, not really. It’s working. You have to work on paper and this is the paper. Okay?”¹

We do not, in physical reality, manipulate formal objects. We interact with squiggles on paper, a whiteboard, or a screen. Taking seriously the observable details of what we do there helps unravel the mysteries of formalism’s role in rationality, and how and when and why rationality works.

There’s two tricks to formality: concrete proceduralization and decontextualization. These are accomplished using external, culturally produced, mostly-recent technologies that allow us to repurpose brains evolved for mere reasonableness to do rationality. (My analysis here draws heavily on Catarina Dutilh Novaes’ Formal Languages in Logic.)

Concrete proceduralization: factoring a polynomial on paper involves visual routines, seeing-as, hand-eye coordination, trouble repair, and—in sum—much the same interactional dynamics as any other routine, concrete activity. That’s pretty much all we’re capable of! We rely on the material aid (paper and ink) as a cognitive prosthesis. Writing and reading what we have written more-or-less accomplishes abstract formal inference. This is an astonishing triumph of embodied, cultural practices of notation. The material outputs of this externally-observable rationality causally affect physical situations, via our subsequent activities that take into account what we have written.

Decontextualization enforces a rational closed-world idealization. We evolved to maintain open awareness of unenumerable potentially relevant factors. Surrounded by a buzzing cloud of distracting possibilities, we are incapable of focusing for rational inference—without external prostheses that shield us from the noise. Rationality gains its power from transcending context, purpose, specifics, to create universal, abstract, general systems. The meaninglessness of x is the key to that power. Nothing is relevant to it.

Getting better at solving problems by understanding abstractions better is a major aspect of advanced rationality—not meta-rationality. Meta-rationality is mainly concerned with the context within which rationality operates. But, that includes the material context within which we do formal work. Improvements in notation, to make the concrete visual work of formula manipulation easier, are a meta-rational topic, for example.

What makes rationality work?

We do.

The wording of the question might sound odd. “Why does rationality work?” might sound more natural. That’s rationalism’s central question—with the hope that there’s some elegant, abstract, universal answer that explains why it always does and must work. Unfortunately, there isn’t one. Rationality works only when we do work to make it work. We do unenumerably many different sorts of work, and they don’t always work; so no elegant, abstract, universal explanation is possible. Still, there’s much to say about sorts of work we do. This chapter covers several.

Circumrationality

Part One explained why formal rationality cannot make contact with nebulous reality. A rational system refers to objects, categories, properties, and relationships that it cannot define, and cannot explain how to identify as concrete phenomena. Disconnection from reality is how rationality gains its power: it is our knowing to leave nebulosity out of a formal problem—where it would wreck rational inference—that lets us solve it.

However, that means we have to act as the dynamic interface that bridges a formalism/reality gap. Circumrationality is this non-rational work we do at the margins of a rational system. Actualizing a correspondence between rationally specified entities and the messy real world requires perception and interpretation, action and improvisation, communication and negotiation. How do we find the entities a rational plan refers to? How do we describe the mess we find in the terms the system restricts itself to? How do we “take” the actions it mandates?

(Bowker and Star’s Sorting Things Out is an entire book devoted to what I call circumrationality, with many detailed and fascinating examples, some of which I’ll probably reuse.)

What counts as a missing band in an electrophoresis gel? What counts as a vacuum seal? Such considerations may be quantified, standardized, rationalized; but not every detail ever can be. Where the rational system falls silent, reasonable perception and judgement is required. That involves the kinds of dynamics of interaction explained in Part Two.

Circumrationality treats vagueness, uncertainty, and nebulosity as specific practical difficulties to be addressed with unenumerable specific methods, suitable in specific situations.

Routine reasonable repair is required when rationality glitches. When that succeeds, it goes unnoticed, and rationality takes the credit.

Circumrationality may work more or less well. A major meta-rational task is revising the rationality/circumrationality relationship when it isn’t working well, or if you notice opportunities for improvement. If the participants in a rational system frequently find it difficult to classify objects according to its ontology, or cannot figure out how to take the actions it requires because they don’t seem meaningful in context, it’s time to get meta-rational. Maybe circumrationality needs upgrading: better tools or skills might enable more accurate classification, for example. Maybe the rational system requires rethinking. Is the ontology adequate for its purposes? Most often, rationality and circumrationality should both be reworked to work better together.

Procedural systems

Procedural systems eliminate the need for novel problem solving, which is inherently slow and unreliable. They mandate rules for action that cover all likely eventualities within their domain. The norms of a procedural system are similar to those of a formal system, but operate in the material world. Like Newton’s root-finding method, you can “execute” a laboratory protocol “by the book,” and it’s more-or-less unambiguous whether or not you have done so.

Meta-rationality reflects on a procedural system’s adequacy. What would happen if unknown unknowns trip it up, for instance?

Sanity-checking

Sanity-checking formal inference rejects nonsense results from feeding sort-of truths into rational inference. Sort-of truths are usually the only ones available, but the correctness of rational inference depends on absolute truth. We have to accept that rationality often comes to wrong conclusions, for instance when a closed-world idealization fails. When your statistical analysis determines with high confidence that the moon is made of green cheese, you should not rush to publish your exciting discovery.

Meta-rationality reasons about how specific systems of formal reasoning behave in the face of nebulosity.

Standardization

Rationalism highlights methods of adjusting a theory to better fit reality—which is indeed important. However, in practice, much more rational work adjusts reality to fit a rational system. This is true even when the ultimate aim is theory improvement. Using esoteric equipment and methods to get some tiny bit of reality to behave according to theory is most of what you do in a science lab.

Standardization is work that reworks the physical world to make it more nearly fit a rational ontology. Without technological aids, rationality gains little purchase on the natural world at the eggplant scale. You can’t build much of anything out of stuff you find in the wilderness, because the matter has no definite properties. Engineering requires starting materials and components that conform to rational criteria, which enables rational inference. We’ve bootstrapped technological civilization by building ever-more-definite machines that can produce ever-more-definite inputs for building even-more-definite machine-making machines.

Designing standards involves meta-rational reasoning about the consequences of nebulous slop in systems’ inputs. Not just “how much can this system tolerate”—which might be addressed rationally—but “what new design possibilities could new standards enable?”

Shielding

Shielding isolates a situation from factors a rational framework ignores, so its closed-world idealization more nearly holds. We might also describe it as “relevance control”: shielding makes as many of the unenumerable potentially relevant factors as irrelevant as possible.

Shielding can be literal: enclosing a situation in a causally-inert solid material. It can be accomplished many other ways:

Although none of the [scanning tunneling microscopy] lab members would require daily cleaning of the laboratory as an indispensable condition for experimental physics to proceed, a cleaning woman would make her daily rounds, wiping the floor and emptying the garbage bins. Every day at around 4.30 pm, she would wipe the corridor first and then enter the experimental areas of the lab, both upstairs and downstairs. To avoid her touching the cryostats with the floor mop, the lab chief had suggested setting up chains around them. One day, peering down at her wiping the basement floor, he noticed her passing the mop below the chain, thus touching the cryostat, lightly but repeatedly (with each cryostat contact risking a tip crash). To prevent that unexpected “Limbo” move, lab members would set up additional warning signs, some of which were in Spanish, the mother tongue of the cleaning woman (since she had an all-access key, simply locking the doors wouldn’t suffice).²

Shielding limits the need for inference, through context engineering. Unrestricted rational inference doesn’t work, because the premises are not absolutely true, but with adequate shielding you can get a few carefully-chosen steps to work reliably-enough.

The closely-related engineering principle of modularity, or “nearly-decomposable systems,” minimizes the mutual relevance of parts of a complex system, making design and analysis easier.

Meta-rationality can help figure out what sorts of shielding a system needs.

Yes, but why does rationality work?

For different reasons in different cases. We do lots of different things to make rationality work; in each case it’s pretty obvious why it works, but there’s no general explanation.

“But why is it possible at all?”

Well, if you insist on abstract metaphysics, because the world is patterned as well as nebulous. We can’t force reality to conform to some arbitrary system of rationality. Often rationality doesn’t work.

When rationality works, it’s because we’ve found ways of cooperating with patterning to make rationality work well enough in some situations.That’s often a meta-rational activity.

Case studies

Part Three will include many brief examples, and at least two detailed case studies.

Experimental physics

Most of the work is bullying balky equipment into behaving itself.

Phillipe Sormani’s Respecifying Lab Ethnography describes events in the construction and use of a superconducting scanning tunnelling microscope that illustrate most of the points I make in Part Three. The difference between theory and practice is greater in practice than in theory. STM operation involves unexpected birds’ nests in the cabling, mosquitos in the sample chamber, and mops banging the cryostat. Examples of circumrationality, standardization, procedural systems, sanity-checking, and shielding all appear in Sormani’s book.

Park Doing’s Velvet Revolution at the Synchrotron is a first-hand account of the operation of the X-ray source of a football-field-sized particle accelerator. He was responsible for the machine’s maintenance, and vividly describes the messy realities of making this extreme technology work.

Photocopier repair

Julian E. Orr’s Talking about Machines: An Ethnography of a Modern Job is a detailed ethnomethodological study of circumrationality in professional technical work.

The book describes the work of Xerox copier repair technicians. The rational systems they make work are (1) the operation of high-tech, rationally-engineered office equipment, and (2) the formal relationships between Xerox, customer companies that run the copiers, and the technicians themselves.

The engineers designing the copiers had little knowledge of how they were used in practice. Their products worked great in the lab. In the real world, they broke down every few days or at most weeks, and a Xerox technician had to drive to the customer site to repair them. The design engineers did not take into account relevant, uncontrollable context: customers ran them too much or too little, too sporadically, loaded supplies upside down, put in the wrong kind of toner to save money, pushed the wrong button, forgot to remove staples, housed the copiers in unventilated rooms where they overheated, squirted oil in random holes in hope of fixing the machine when it broke down, …

Xerox supplied the repair technicians with manuals with detailed instructions for how to diagnose and repair failures. These manuals were written rationally, from first principles, on the basis of what engineers thought might go wrong, rather than what did go wrong in practice. Often they were unusable, due to not covering common failure modes, giving instructions that made no sense or that were physically impossible to carry out, suggesting a fix that would work but was more complicated or expensive than the practical one; or being outright false.

Circumrationality bridges the unavoidable gap between a tidy rational system and the nebulosity of reality. A copier malfunction report is highly nebulous. Is it actually not working, or is the customer confused? Is it not working because it is broken or because its environment is hostile? If it is broken, what is wrong with it? This is initially uncertain and may never be definable. Copiers are enormously complex, and even individual design engineers do not understand every aspect of one. Taking bits apart, cleaning them, and putting them back together may solve the problem without your ever knowing what actually caused it.

Repairing a copier is usually improvisational; the rational plan in the manual won’t work. It’s done by finger-feel and by ear and by eye, as well as by constructing a plausible causal narrative from practical experience and reflection on a pattern of symptoms.

Orr’s investigation led to a major meta-rational remodeling, which I’ll use as a case study in Part Four. Xerox eventually accepted that technicians’ experience, understanding, and improvisational fixes were critical. Its computer science laboratory PARC built a wiki-like system that let technicians exchange this knowledge globally. The system produced $15 million per year in savings for the company, as problems were diagnosed faster (decreasing labor costs), more accurately (so fewer expensive replacement parts required), and more reliably (so the machines broke down less often, making customers happier).

Advanced rationality

This chapter will cover types of work that remain within a rational system, but which go beyond the “basic” rationality that can be taught explicitly, and that is theorized by rationalisms. I’ll call this “advanced rationality.” You get a glimpse of advanced rationality as an undergraduate. Mostly you learn it at the graduate level, or through mentorship in employment, although it’s mainly transmitted only implicitly.

Advanced rationality shades into meta-rationality, which is why it’s important to cover it in this Part: we’re setting up for the explanation of meta-rationality in Part Four.

Advanced rationality relaxes formalism’s narrowing and shielding of inference. Proceduralization and context-stripping make basic rationality work, but also make it weak and brittle.

Non-procedural rationality

Not all formal problems have procedural solution methods. Sometimes no method is known; sometimes it’s provable there are none; sometimes the available methods are impractical.

You may first encounter this difficulty in a differential equations course. It does not give you a reliable solution method; it teaches many methods, one of which might work. It is not always obvious which, and it is not always obvious how to apply one. Sometimes you have to apply several methods to a single problem, in the right order and in the right ways. How do you figure that out? The textbook doesn’t say. Somewhere in the fine print, it admits that sometimes no method works. This is not yet an encounter with nebulosity, but it may induce a similar feeling of groundlessness.

Beyond differential equations, “prove this theorem,” “devise an experiment to answer this question,” and “design a device that accomplishes this mechanical task” are unboundedly open-ended—while still staying mainly within the realm of the merely rational.

There is no “how” to solving such problems. There are many “hows,” many methods, which might somehow be made relevant, and might work—but any one trick may probably do only part of the work, if it works at all. A solution may involve fitting several together in a novel arrangement. In particularly difficult cases, it may require inventing an altogether new method.

In advanced rationality, a solution may be only a solution, one among many possible—whereas in basic rationality usually there is only the solution. Is the solution you found a good one? Good enough? How do you judge that? Is it worth looking for a better one? Or there may be no solution; and there may be no way of knowing that for sure. How do you decide when to give up?

These are questions of purpose, which, like other context, rationality strips off problem statements. Advanced rationality may address them successfully in an optimization framework. Often they are better treated meta-rationally.

Envisioning

When the topics I describe as “advanced rationality” are discussed, it’s usually in terms of “intuition” or “creativity.” Those translate to “don’t ask how to do this.”

An activity I’ll call envisioning, for lack of a standard term, often comes up when someone is willing to answer. Envisioning is related to, but significantly distinct from, mental visual imagery. It is difficult to describe, and may sound dubious when I explain it.

There seems to be a peculiar taboo involved. I have informally asked many people how they solve advanced rational problems, and explicit reluctance is common. It’s embarrassing, even for people with acknowledged professional expertise in rationality. I’ve heard that it’s too personal, like talking specifically about your experience of sex. Many feel vulnerable because they suspect they are bad at it, or doing it wrong, because they had to figure it out entirely privately—since there is a taboo against talking about it! “Probably real mathematicians know how to do it right; I’m just faking it.” Even Richard Feynman felt he had to apologize awkwardly for doing it badly; he called it “a half-assedly thought-out pictorial semi-vision thing.”

I would perpetuate the taboo, perhaps, except that envisioning becomes even more important in meta-rationality. Explaining it first as an aspect of advanced rationality may prevent the impression that it’s pure woo.

Let’s give it some initial credibility by quoting Albert Einstein:

“The words or the language, as they are written or spoken, do not seem to play any role in my mechanism of thought. The psychical entities which seem to serve as elements in thought are certain signs and more or less clear images which can be “voluntarily” reproduced and combined. There is, of course, a certain connection between those elements and relevant logical concepts. It is also clear that the desire to arrive finally at logically connected concepts is the emotional basis of this rather vague play with the above-mentioned elements. But taken from a psychological viewpoint, this combinatory play seems to be the essential feature in productive thought—before there is any connection with logical construction in words or other kinds of signs which can be communicated to others.

The above-mentioned elements are, in my case, of visual and some of muscular type. Conventional words or other signs have to be sought for laboriously only in a secondary stage, when the mentioned associative play is sufficiently established and can be reproduced at will.³

Accounts typically emphasize that envisioning is somewhat like deliberately imagined visual images, but different in respects that are consistent across reports. One is that envisioning also resembles kinesthetic experience—what Einstein describes as a “muscular” or “motor” quality. Another is that it lacks aspects of visual experience: envisioning is typically described as vague, and the forms are “ghostly,” colorless, and transparent. Instead, this “semi-vision thing” seems more a direct apperception of shapes hanging in space, and particularly the dynamic relationships among them. Further, one can act upon them oneself—play with them, as Einstein says—and observe the consequences. Envisioning is productive when the analogy between this imagined activity and a formal problem leads to a formal solution, when translated into words or formal notation.

(This is the sense in which the rationalist fantasy of entering the Platonic realm is “not entirely wrong.” It probably has much more to do with the internalization of visuo-motor routines than metaphysics, however.)

Whereas, in advanced rationality, envisioning enables you to “feel for” a solution, meta-rationality uses envisioning to feel for a problem. Problem-finding is a major meta-rational operation. In other meta-rational activity, we feel for new ontologies and envision assemblages of systems. Before intervening meta-rationally in a rational system, we envision the consequences.

Ascending the J-curve

It is possible to ignore context, purpose, and nebulosity throughout a career as a technical professional. There’s nothing wrong with that; competent problem-solvers are valuable, and brilliant ones more so. However, your usefulness in that case depends on other people doing the work of abstracting formal problems from reality, and figuring out how to turn your formal solutions into practical work products.

Typically, moving into more senior positions brings you closer to the volatile, ambiguous, unknowable complexities of reality. Increasingly, it is your job to make decisions about purposes and priorities; to turn nebulous messes into crisp problems you delegate to junior staff who can do basic, cut-and-paste rationality; to translate “solutions” into practical activities.

Advanced rationality, then, recognizes that solving difficult problems requires multiple models, exploiting ad hoc domain constraints, inference-limiting, and solution-monitoring. Understanding when and why formal procedures work becomes ever-more important.

Practitioners of advanced rationality are likely to say:

• Maybe there’s another way of looking at this
• All models are wrong, but some are useful
• It’s publishable, and probably even true
• That’s a beautiful textbook theory, and it won’t work here
• Good, fast, cheap: pick two
• It does what the client needs, so we’re ignoring the general case
• The design was correct last year. It’s incorrect today. Start over
• You should know how to prove theorems, and you should be skeptical that theorems prove anything

These slogans shade into meta-rationality; but they may still be working primarily within a rational system.

Advanced rationality vs. meta-rationality

The boundary is nebulous, but it is also worth making the distinction.

Advanced rationality works mainly within a rational system, which it takes mainly for granted. You do not question the ontology the system assumes. Which methods to apply, and how, is up for grabs, but you do not consider using ones from an entirely different system. You do not consider switching overall to a different system, nor bringing several diverse ones to bear. It does not occur to you to apply ethnomethodology to an office equipment reliability problem, or evolutionary biology to a mechanical engineering problem.

How to not be an oblivious geek

Julia Galef: Hm, can you give me a real-world example?
Mathematician: Sure! OK, so imagine you have an infinite number of boxes with ducks in them…

Being an “oblivious geek” means doing rationality badly because you fail to recognize its limits.

You may be oblivious to context. You take a closed-world idealization for granted, and deliberately blind yourself to evidence that it isn’t working well. You do not notice when, in a particular situation, it excludes critical relevant factors that render it dysfunctional. The ontology of the rational system you inhabit may fail to make relevant distinctions that success would depend on.

You may fail to reflect on purposes. Mere rationality generally takes those as immutable givens. Someone else supplies you with problems; it’s your job to solve them. You do not ask why. Are they good problems to solve? If you are oblivious to that meta-rational question, you may come to regret having used your technical abilities to make the world worse.

Another way of defining “oblivious geeking”: it is the failure to make meta-rational choices explicitly. All rational work involves meta-rational options: how will you characterize the real-world problem situation? What sorts of technical methods will you apply? Specifically how will you apply them?

Mostly we make these choices mindlessly, implicitly applying defaults from our community of practice. Mostly, professionals want to stick to their professional competence and solve well-defined problems within that domain using standard methods. This is inadequate and sometimes leads to sometimes-catastrophic failures.

If you are a macroeconomist, you take “aggregate demand” for granted as a fundamental ontological category, even though you may vaguely remember it’s “theoretically problematic.” You take for granted that, whatever you are working on, you will apply differential equations, because that’s the main formal system your field uses. Macroeconomics has little if any predictive value; what justifies its practice? Oblivious geekery allows you to ignore the question.

This chapter will suggest ways to notice that you are being an oblivious geek, and remedies.

Overall, the antidote is: meta-rationality. That is, reflection on how you are doing rationality. So this last chapter of Part Three is the bridge into Part Four, which is about that.